字符串匹配 - 模式预处理:KMP 算法(Knuth-Morris-Pratt)
Knuth-Morris-Pratt算法(简称KMP)是最常用的字符串匹配算法之一。@pdai
算法简介
如下算法解释主要来源于这里,但是通常很难阅读完全,我推荐你直接进入下一节 图例解释部分。
我们来观察一下朴素的字符串匹配算法的操作过程。如下图(a)中所描述,在模式 P = ababaca 和文本 T 的匹配过程中,模板的一个特定位移 s,q = 5 个字符已经匹配成功,但模式 P 的第 6 个字符不能与相应的文本字符匹配。
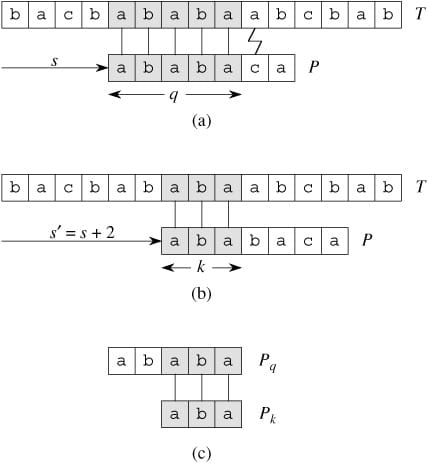
此时,q 个字符已经匹配成功的信息确定了相应的文本字符,而知道这 q 个文本字符,就使我们能够立即确定某些位移是非法的。例如上图(a)中,我们可以判断位移 s+1 是非法的,因为模式 P 的第一个字符 a 将与模式的第二个字符 b 匹配的文本字符进行匹配,显然是不匹配的。而图(b)中则显示了位移 s’ = s+2 处,使模式 P 的前三个字符和相应的三个文本字符对齐后必定会匹配。KMP 算法的基本思路就是设法利用这些已知信息,不要把 "搜索位置" 移回已经比较过的位置,而是继续把它向后面移,这样就提高了匹配效率。
The basic idea behind KMP’s algorithm is: whenever we detect a mismatch (after some matches), we already know some of the characters in the text (since they matched the pattern characters prior to the mismatch). We take advantage of this information to avoid matching the characters that we know will anyway match.
已知模式 P[1..q] 与文本 T[s+1..s+q] 匹配,那么满足 P[1..k] = T[s’+1..s’+k] 其中 s’+k = s+q 的最小位移 s’ > s 是多少?这样的位移 s’ 是大于 s 的但未必非法的第一个位移,因为已知 T[s+1..s+q] 。在最好的情况下有 s’ = s+q,因此立刻能排除掉位移 s+1, s+2 .. s+q-1。在任何情况下,对于新的位移 s’,无需把 P 的前 k 个字符与 T 中相应的字符进行比较,因为它们肯定匹配。
可以用模式 P 与其自身进行比较,以预先计算出这些必要的信息。例如上图(c)中所示,由于 T[s’+1..s’+k] 是文本中已经知道的部分,所以它是字符串 Pq 的一个后缀。
此处我们引入模式的前缀函数 π(Pai),π 包含有模式与其自身的位移进行匹配的信息。这些信息可用于避免在朴素的字符串匹配算法中,对无用位移进行测试。
π[q] = max {k : k < q and Pk ⊐ Pq}
π[q] 代表当前字符之前的字符串中,最长的共同前缀后缀的长度。(π[q] is the length of the longest prefix of P that is a proper suffix of Pq.)
下图给出了关于模式 P = ababababca 的完整前缀函数 π,可称为部分匹配表(Partial Match Table)。
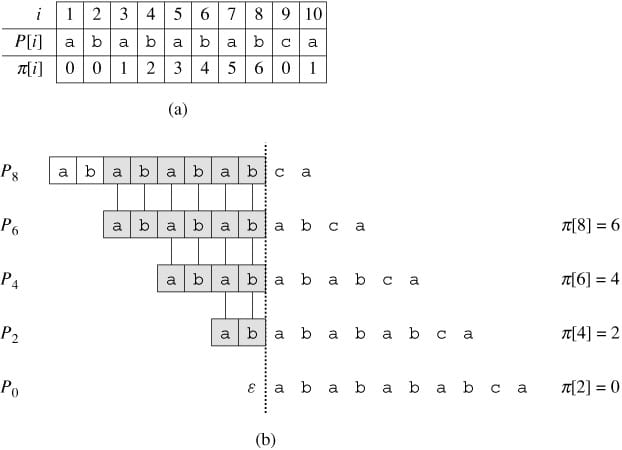
计算过程:
- π[1] = 0,a 仅一个字符,前缀和后缀为空集,共有元素最大长度为 0;
- π[2] = 0,ab 的前缀 a,后缀 b,不匹配,共有元素最大长度为 0;
- π[3] = 1,aba,前缀 a ab,后缀 ba a,共有元素最大长度为 1;
- π[4] = 2,abab,前缀 a ab aba,后缀 bab ab b,共有元素最大长度为 2;
- π[5] = 3,ababa,前缀 a ab aba abab,后缀 baba aba ba a,共有元素最大长度为 3;
- π[6] = 4,ababab,前缀 a ab aba abab ababa,后缀 babab abab bab ab b,共有元素最大长度为 4;
- π[7] = 5,abababa,前缀 a ab aba abab ababa ababab,后缀 bababa ababa baba aba ba a,共有元素最大长度为 5;
- π[8] = 6,abababab,前缀 .. ababab ..,后缀 .. ababab ..,共有元素最大长度为 6;
- π[9] = 0,ababababc,前缀和后缀不匹配,共有元素最大长度为 0;
- π[10] = 1,ababababca,前缀 .. a ..,后缀 .. a ..,共有元素最大长度为 1;
KMP 算法 KMP-MATCHER 中通过调用 COMPUTE-PREFIX-FUNCTION 函数来计算部分匹配表。
KMP-MATCHER(T, P)
n ← length[T]
m ← length[P]
π ← COMPUTE-PREFIX-FUNCTION(P)
q ← 0 //Number of characters matched.
for i ← 1 to n //Scan the text from left to right.
do while q > 0 and P[q + 1] ≠ T[i]
do q ← π[q] //Next character does not match.
if P[q + 1] = T[i]
then q ← q + 1 //Next character matches.
if q = m //Is all of P matched?
then print "Pattern occurs with shift" i - m
q ← π[q] //Look for the next match.
COMPUTE-PREFIX-FUNCTION(P)
m ← length[P]
π[1] ← 0
k ← 0
for q ← 2 to m
do while k > 0 and P[k + 1] ≠ P[q]
do k ← π[k]
if P[k + 1] = P[q]
then k ← k + 1
π[q] ← k
return π
预处理过程 COMPUTE-PREFIX-FUNCTION 的运行时间为 Θ(m),KMP-MATCHER 的匹配时间为 Θ(n)。
相比较于 NAIVE-STRING-MATCHER,KMP-MATCHER 的主要优化点就是在当确定字符不匹配时对于 pattern 的位移。
NAIVE-STRING-MATCHER 的位移效果是:文本向后移一位,模式从头开始。
s = s - j + 1;
j = 0;
KMP-MATCHER 首先对模式做了获取共同前缀后缀最大长度的预处理操作,位移过程是先将模式向后移 partial_match_length - table[partial_match_length - 1],然后再判断是否匹配。这样通过对已匹配字符串的已知信息的利用,可以有效节省比较数量。
if (j != 0)
j = lps[j - 1];
else
s++;
下面描述了当发现字符 j 与 c 不匹配时的位移效果。
// partial_match_length - table[partial_match_length - 1]
rrababababjjjjjiiooorababababcauuu
||||||||-
ababababca
// 8-6=2
rrababababjjjjjiiooorababababcauuu
xx||||||-
ababababca
// 6-4=2
rrababababjjjjjiiooorababababcauuu
xx||||-
ababababca
// 4-2=2
rrababababjjjjjiiooorababababcauuu
xx||-
ababababca
// 2-0=2
rrababababjjjjjiiooorababababcauuu
xx-
ababababca
综上可知,KMP 算法的主要特点是:
- 需要对模式字符串做预处理;
- 预处理阶段需要额外的 O(m) 空间和复杂度;
- 匹配阶段与字符集的大小无关;
- 匹配阶段至多执行 2n - 1 次字符比较;
- 对模式中字符的比较顺序时从左到右;
算法图例
如下是阮一峰根据Jake Boxer的文章总结的图例。
下面,我用自己的语言,试图写一篇比较好懂的KMP算法解释。

首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。

因为B与A不匹配,搜索词再往后移。

就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
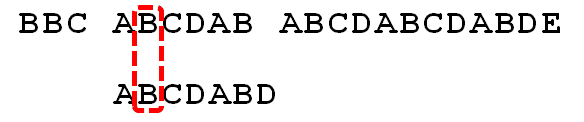
接着比较字符串和搜索词的下一个字符,还是相同。

直到字符串有一个字符,与搜索词对应的字符不相同为止。
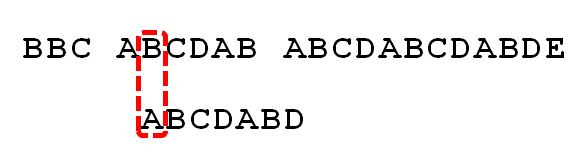
这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
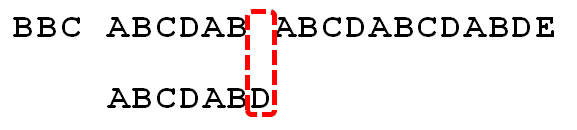
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
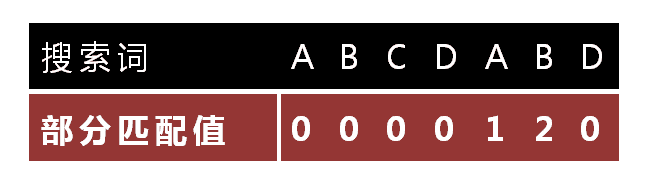
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
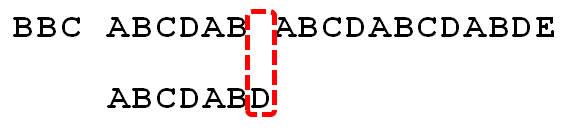
已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
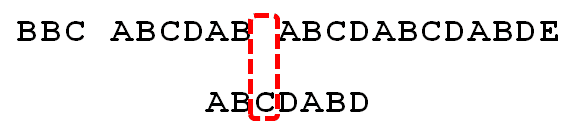
因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
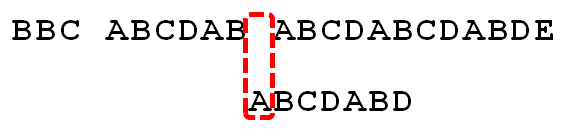
因为空格与A不匹配,继续后移一位。

逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。

下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
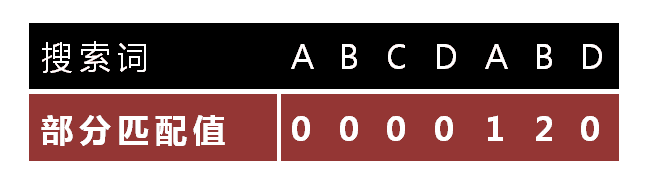
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。

"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
参考文章
- http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/
- https://www.cnblogs.com/gaochundong/p/string_matching.html#kmp_string_matching_algorithm
- http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html